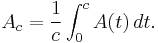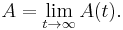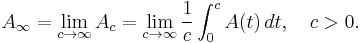Availability

In telecommunications and reliability theory, the term availability has the following meanings:

For example, a unit that is capable of being used 100 hours per week (168 hours) would have an availability of 100/168. However, typical availability values are specified in decimal (such as 0.9998). In high availability applications, a metric known as nines, corresponding to the number of nines following the decimal point, is used. In this system, "five nines" equals 0.99999 (or 99.999%) availability.

Contents

Availability in Layman's Terms

Availability of a system over its life-cycle is typically measured as a factor of its reliability - as reliability increases, so does availability. However, no system can guarantee 100.000% reliability; and as such, no system can assure 100.000% availability. Further, reliability engineering and maintainability involve processes designed to optimize availability under a set of constraints, such as time and cost-effectiveness. Availability is the goal of most system users, and reliability engineering and maintainability provide the means to assure that availability performance requirements are achieved.

Representation

The most simple representation for availability is as a ratio of the expected value of the uptime of a system to the aggregate of the expected values of up and down time, or

A = \frac{E[\mathrm{Uptime}]}{E[\mathrm{Uptime}]%2BE[\mathrm{Downtime}]}

If we define the status function 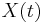X(t) as

X(t)= \begin{cases} 1, & \mbox{sys functions at time } t\\ 0, & \mbox{otherwise} \end{cases}

therefore, the availability A(t) at time t>0 is represented by

A(t)=\Pr[X(t)=1]=E[X(t)].

Average availability must be defined on an interval of the real line. If we consider an arbitrary constant 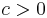c>0, then average availability is represented as

A_c = \frac{1}{c}\int_0^c A(t)\,dt.

Limiting (or steady-state) availability is represented by

A = \lim_{t \rightarrow \infty} A(t).

Limiting average availability is also defined on an interval (0,c] as,

A_{\infty}=\lim_{c \rightarrow \infty} A_c = \lim_{c \rightarrow \infty}\frac{1}{c}\int_0^c A(t)\,dt,\quad c > 0.

Example

If we are using equipment which has mean time to failure (MTTF) of 81.5 years and mean time to repair (MTTR) of 1 hour:

MTTF in hours = 81.5*365*24=713940

Availability= MTTF/(MTTF+MTTR) = 713940/713941 =99.999859%

Unavailability = 0.000141%

Outage due to equipment in hours per year

U=0.01235 hours per year.

Literature

Availability is well established in the literature of stochastic modeling and optimal maintenance. Barlow and Proschan [1975] define availability of a repairable system as "the probability that the system is operating at a specified time t." While Blanchard [1998] gives a qualitative definition of availability as "a measure of the degree of a system which is in the operable and committable state at the start of mission when the mission is called for at an unknown random point in time." This definition comes from the MIL-STD-721. Lie, Hwang, and Tillman [1977] developed a complete survey along with a systematic classification of availability.

Availability measures are classified by either the time interval of interest or the mechanisms for the system downtime. If the time interval of interest is the primary concern, we consider instantaneous, limiting, average, and limiting average availability. The aforementioned definitions are developed in Barlow and Proschan [1975], Lie, Hwang, and Tillman [1977], and Nachlas [1998]. The second primary classification for availilability is contingent on the various mechanisms for downtime such as the inherent availability, achieved availability, and operational availability. (Blanchard [1998], Lie, Hwang, and Tillman [1977]). Mi [1998] gives some comparison results of availability considering inherent availability.

Availability considered in maintenance modeling can be found in Barlow and Proschan [1975] for replacement models, Fawzi and Hawkes [1991] for an R-out-of-N system with spares and repairs, Fawzi and Hawkes [1990] for a series system with replacement and repair, Iyer [1992] for imperfect repair models, Murdock [1995] for age replacement preventive maintenance models, Nachlas [1998, 1989] for preventive maintenance models, and Wang and Pham [1996] for imperfect maintenance models.

See also

References

 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).

External links